Grundlagen zum Widerstand

Widerstände werden beispielsweise dazu verwendet, um LEDs sanft zum Leuchten zu bringen.

Um eine LED (Licht emittierende Diode) zu beleuchten, ist es erforderlich, dass eine Spannung von 2 V über ihre beide Klemmen angewendet wird. Aus diesem Grund reicht die Spannung nicht aus, um die LED mit einer einzigen Trockenzelle (circa 1,5 V), wie in Abb. 1 (a) dargestellt zu erleuchten. Wenn stattdessen zwei Trockenzellen in Serie verbunden werden, wie in Abb. 1 (b) dargestellt, ist die Spannung von circa 3 V zu viel und der überschüssige Strom fließt durch die LED und zerstört diese damit. Wenn zwischen der LED und der Trockenzelle wie in Abb. 1 (c) dargestellt ein passender Widerstand platziert wird, leuchtet die LED mit einer angemessenen Helligkeit auf, ohne dass weder auf die LED noch auf die Batterien eine übermäßige Last angewendet wird. Der Widerstand führt somit dazu, dass die elektrischen Schaltkreise sanft laufen, indem der Fluss des elektrischen Stromes eingeschränkt wird, und ist somit eine essentielle Komponente in einem jeden elektrischen Schaltkreis.

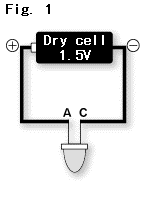
(a) Keine Lichtemission

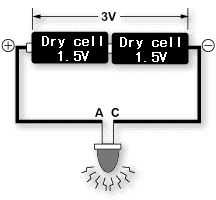
(b) Es fließt zu viel Strom

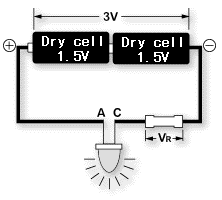
(c) Ideale Betriebsbedingung

Lassen Sie uns das Ohm'sche Gesetz noch einmal genauer betrachten.

Im letzten Beispiel haben wir die Nutzung eines passenden Widerstands erwähnt, um den elektrischen Schaltkreis zu betreiben. Lassen Sie uns nun einen genaueren Blick darauf werfen, wie der erforderliche, angemessene Widerstandswert bestimmt werden kann. Dies erfolgt im Rahmen des Ohm'schen Gesetzes, dass besagt, dass die Spannung V und der Strom I durch die folgende Gleichung im Verhältnis zueinander stehen: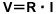
…(1)
Hier ist R die proportionale Konstante der Spannung V zum Strom I und wird elektrischer Widerstand oder nur Widerstand genannt (Einheit:Ω). Ein Widerstand ist einfach dieser Widerstand als elektrische Komponente umgesetzt.

Was ist nun die Größe des Widerstands in Abb. 1 (c)?

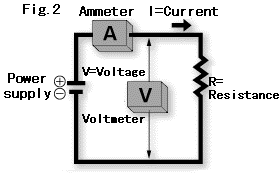
Lassen Sie uns nun über die Bedeutung des Ohm'schen Gesetzes nachdenken. Im Schaltkreis von Abb. 2 beläuft sich der Widerstand R, wenn wir davon ausgehen, dass die Spannung V 1 V und der Strom I 1 A beträgt, gemäß der Gleichung (1) auf der vorherigen Seite, auf:

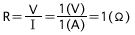
Das heißt 1&Omega-Widerstand ist ein Widerstand, durch den ein Strom von 1 A fließt, wenn eine Spannung von 1 V auf diesen angewendet wird. Oder ein Widerstand, der eine Spannung von 1 V auf diesem erzeugt, wenn ein Strom von 1 A diesen durchläuft. Wenn die Spannung dieselbe Spannung von 1 V bleibt, der Strom aber 0,2 A beträgt, lautet der erforderliche Spannungswert:

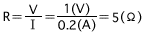
Ferner wird die Spannung, die erforderlich ist, damit ein Strom von 1 A durch einen 5&Omega-Widerstand laufen kann, in der folgenden Gleichung dargelegt:

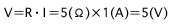
Daher ist das Ohm'sche Gesetz in einem elektrischen Schaltkreis immer erfüllt; wenn die Werte von jeweils zwei beliebigen Elementen aus Spannung, Strom und Widerstand bekannt sind, ist es demnach möglich, den Wert des verbleibenden Parameters zu bestimmen.

Lassen Sie uns nun einen Blick auf den Wert des Widerstands werfen, der in dem Beispiel von Abb. 1 (c) erforderlich ist. Wenn die LED normal betrieben wird, beläuft sich die Spannung über diese beiden Klemmen auf circa 2 V. Wenn man die Spannung von 2 V über die beiden Klemmen der LED von der Batteriespannung von 3 V abzieht, erhalten wir die Spannung VR über die beiden Klemmen des Widerstands wie folgt:

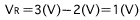
Wenn wir den Strom ILED, der im normalen Betrieb durch die LED läuft, mit 15 mA festlegen (1 mA = 1/1000 A), dann lautet der erforderliche Widerstandswert R gemäß dem Ohm'schen Gesetz wie folgt:

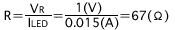
Aus diesem Grund beträgt der Widerstandswert des Widerstands in Abb. 1 (c) 67 Ω.

Leistungsaufnahme und Nennleistung

Wie Menschen Energie zum Arbeiten brauchen, brauchen auch elektrische Geräte wie Motoren, Heizgeräte, Lampen usw. Energie, um betrieben werden zu können. Die Menge der erforderlichen Energieleistungsaufnahme und Nennleistung wird von dem Parameter der Leistungsaufnahme ausgedrückt. Da die elektrische Leistung (selbst diese Leistungsaufnahme) als Produkt der Spannung und des Stroms ausgedrückt wird, erhält man die Leistung P durch die folgende Gleichung:

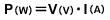
Da gemäß dem Ohm'schen Gesetz eine Spannung über die beiden Klemmen eines Widerstands hinweg auftritt, wenn ein Strom durch diesen läuft, wird selbst in einem elektrischen Gerät wie einem Widerstand Energie verbraucht. Wenn beispielsweise ein Strom von 1 A durch einen Widerstand von 1 Ω läuft und somit eine Spannung von 1 V über den Widerstand hinweg auftritt, gemäß dem Ohm'schen Gesetz, beträgt sich die Leistungsaufnahme:

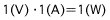
und daher beläuft sich die Leistungsaufnahme im Widerstand auf 1 W. Da bei einem Widerstand diese Leistung komplett als Wärme ausgestrahlt wird, steigt bei einer hohen Leistungsaufnahme die Temperatur des Widerstands selbst an, wodurch dieser letztendlich verbrennt oder schmilzt. Aus diesem Grund muss angegeben werden, bis zu welcher Leistung der Widerstand sicher verbrauchen kann. Diese Leistung wird als Nennleistung des Widerstands bezeichnet. Unter Berücksichtigung des Schutzes vor einem Verbrennen des Widerstands wird ein Widerstand normalerweise bei einer Leistungsaufnahme von weniger als 1/2 der Nennleistung eingesetzt.

Serieller Anschluss und paralleler Anschluss

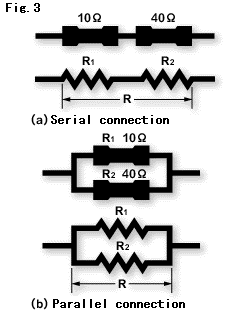
Die Anschlüsse in elektrischen Schaltkreisen lassen sich weitestgehend als serielle Anschlüsse und parallele Anschlüsse klassifizieren, die in Abb. 3 dargestellt werden. Wenn mehrere Widerstände miteinander verbunden werden, unterscheidet sich der kombinierte Widerstandswert in den seriellen und parallelen Anschlüssen wie folgt:

Bei einem seriellen Anschluss: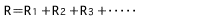

Bei einem parallelen Anschluss: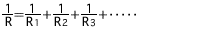

Infolgedessen lauten sich die entsprechenden kombinierten Widerstandswerte in Abb. 3 wie folgt:

(a) Der kombinierte Widerstand bei einem seriellen Anschluss lautet: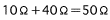

(b) Der kombinierte Widerstand bei einem parallelen Anschluss lautet: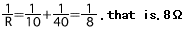

Das heißt, bei einem seriellen Anschluss steigt der kombinierte Widerstandswert, wenn die Anzahl der Widerstände im Anschluss zunimmt, und bei einem parallelen Anschluss nimmt dieser ab, wenn die Anzahl der Widerstände im Anschluss steigt.